১ সংজ্ঞা
শর্টেস্ট পাথ এর সংজ্ঞাটা হবে অনেকটা এরকম - আমার যদি অনেকগুলো শহর থাকে, আর শহরগুলোর মধ্যে যদি অনেকগুলো পথ থাকে, (যেই পথগুলোর একেকটার একেকরকমের দৈর্ঘ্য থাকতে পারে - এবং কোন পথে কোন জ্যাম থাকবে না) তাহলে কোন একটা শহর থেকে অন্য আরেকটা শহরে যেই পথ দিয়ে গেলে সবচে’ কম দূরত্ব যাওয়া লাগবে সেটা হচ্ছে আমার প্রথম শহরটা থেকে দ্বিতীয় শহরটার শর্টেস্ট পাথ।
যখন আমরা গ্রাফ থিওরীর টার্মিনোলজিতে কথা বলি, তখন আমরা শহরগুলোকে শহর না বলে বলি নোড (node), আর পথগুলো পথ না বলে বলি এজ (edge), আর আমরা এই পুরো ম্যাপটাকে বলে গ্রাফ (graph)। টার্মিনোলজি শেখাটা ভোকাবুলারি শেখার মতো, অন্যদের সাথে গ্রাফ থিওরী নিয়ে সহজে কথা বলা যায়।
২ প্রাথমিক ডাটা স্ট্রাকচার
বেশ তো, কিন্তু প্রথমে চিন্তা করো তুমি কিভাবে, কম্পিউটারে ডাটা হিসেবে শহরগুলোর পথগুলোকে রাখবা। সবচে’ সহজভাবে জিনিসটা এভাবে করা যায় - আমি একটা
2D অ্যারে রাখি, distance নামের যেখানে distance[i][j] হবে $i$ তম শহর থেকে $j$ তম শহরে যাওয়ার দূরত্ব।
তো এই ম্যাট্রিক্সটাকে সাধারণত বলা হয় অ্যাডজাসেন্সি ম্যাট্রিক্স (adjacency matrix)।
#define M 100
int distance[M][M];যদি আমাদের গ্রাফে খুব বেশি নোড না থাকে এভাবে ডাটা রাখতে কোন সমস্যা হবে না। কিন্তু অ্যাডজাসেন্সি ম্যাট্রিক্স এর প্রথম সমস্যা হচ্ছে এটা প্রচুর মেমরি নেয়। ধরো তোমার $20,000$টা শহর আছে আর তাদের মধ্য $50,000$ টা পথ আছে। আমার এখানে সবমিলে ডাটা আসলে $50,000$। কিন্তু তুমি যখন অ্যারে ডিক্লেয়ার করতে যাচ্ছো, তোমার $20,000 \times 20,000$সাইজের অ্যারে ডিক্লেয়ার করতে হচ্ছে, যার বেশিরভাগই তুমি ব্যবহার করছো না। আর তোমার মেমরি হয়তো এত জায়গাও নেই। দ্বিতীয় সমস্যা হচ্ছে, তুমি ঠিক জানো না $i$ এর সাথে কোন কোন $j$ তে পথ আছে। তো তোমার সবগুলো $j$ খুঁজে খুঁজে দেখতে হবে সেখান থেকে পথ আছে কি না, যেটা আরো সমস্যা। কারণ এমন হতে পারে $i$ নাম্বার শহরটার শুধু একটা শহরের সাথে পথ আছে, আর সেটা আছে সবার শেষ ইন্ডেক্সটাতে। তো এই ক্ষেত্রে আমরা প্রচুর সময় নষ্ট করবো পথ খুঁজতে।
সহজ উপায় হচ্ছে আমরা দুটো ভেক্টরের অ্যারে রাখতে পারি। ধরো প্রথমটার নাম হচ্ছে edge, দ্বিতীয়টার নাম হচ্ছে cost।
#define M 100
vector<int> edge[M], cost[M];edge[i] তে থাকবে সবগুলো নোড যাদের i এর সাথে পথ আছে, আর cost[i] তে থাকবে, যথাক্রমে সেই পথগুলোর দূরত্ব।
মানে ধরো edge[i] এর প্রথম এলিমেন্টটা যদি $23$ হয় তাহলে cost[i] এর প্রথম এলিমেন্টটা হবে i থেকে
নোড $23$ এর দূরত্ব।
৩ ব্রেডথ ফার্স্ট সার্চ (Breadth First Search (BFS))
তোমার যদি রিকার্শন জানা থাকে তুমি DFS চালিয়ে দিতে পারো গ্রাফ এর উপর শর্টেস্ট পাথ বের করার জন্য। কিন্তু রিকার্শন একটা ঝামেলার হয়ে যায় আসলে, প্রচুর ফাংশন কল আর ডিপেন্ডেন্সির কারণে জিনিসটা স্লো হয়ে যায়।
শর্টেস্ট পাথ বের করার একটা সহজ আর কাজের পদ্ধতি হচ্ছে BFS। BFS লেখা বেশ সোজা, মানে কন্টেস্টের সময়ে খুব দ্রুত লিখে ফেলা যায়। আর তুমি যদি হাল্কা পাতলা অপটিমাইজ করতে পারো তাহলে BFS বেশ দ্রুতই কাজ করবে।
BFS এ আমরা যেটা করি তা হচ্ছে। আমরা একটা কিউ (queue) রাখি, আর একটা দূরত্ব রাখার জন্য অ্যারে রাখি। প্রথমে আমরা ধরে নেই সবার দূরত্ব অসীম, আর শুধু শুরু শহরটার দূরত্ব হচ্ছে শূণ্য। তারপর আমরা কিউতে শুরুর শহরটাকে ঢুকাই।
এরপর যতক্ষণ না কিউ খালি হচ্ছে ততক্ষণ আমরা করি কি কিউর প্রথমে যেই শহরটা আছে, সেটাকে বের করে আনি প্রসেসিং এর জন্য। তারপর ওটা থেকে যেই শহরগুলোতে যাবার পথ আছে সেই শহরগুলোতে যদি আমরা এই শহরটা থেকে যাই তাহলে যদি আগের চেয়ে কম সময় লাগে যেতে আমরা
- সেই শহরটার নতুন দূরত্ব আপডেট করি
- নতুন দূরত্ব পাওয়া শহরটাকে প্রসেস করার জন্য কিউতে পুশ করি।
তারপর যতক্ষণ না পর্যন্ত সব শহরগুলোকে প্রসেস হচ্ছে ততক্ষণ ধরে আমরা আপডেট করতে থাকবো। যদি কোন একটা সময় আপডেট আর করা না যায় (মানে, আমরা কোন শহরের জন্যই এমন কোন নতুন পথ পাচ্ছি না যেটা দিয়ে গেলে ওই শহরটাতে বর্তমান পথটার চেয়ে তাড়াতাড়ি যাওয়া যাবে)
ধরো এই গ্রাফটার জন্য
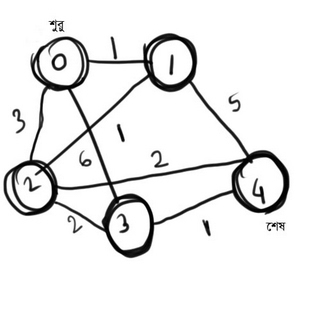
প্রথমে আমরা 0 কে কিউতে পুশ করবো। এখন 0 এর দূরত্ব হচ্ছে 0 আর বাকি সবার দূরত্ব হচ্ছে অসীম।
| শহর | দূরত্ব |
|---|---|
| 0 | 0 |
| 1 | অসীম |
| 2 | অসীম |
| 3 | অসীম |
| 4 | অসীম |
0 থেকে যদি আমি 1 এ যাই, তাহলে 1 এর নতুন দূরত্ব হবে 1। 1 কে প্রসেসিং এর জন্য কিউতে ঢুকাই।
0 থেকে যদি আমি 2 এ যাই, তাহলে 2 এর নতুন দূরত্ব হবে 3। 2 কে প্রসেসিং এর জন্য কিউতে ঢুকাই।
0 থেকে যদি আমি 3 এ যাই, তাহলে 3 এর নতুন দূরত্ব হবে 6। 3 কে প্রসেসিং এর জন্য কিউতে ঢুকাই।
এখন আমাদের কিউ এর অবস্থা এই রকম 1,2,3
| শহর | দূরত্ব |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 3 |
| 3 | 6 |
| 4 | অসীম |
আমরা কিউ এর ডগা থেকে 1 কে বের করে আনবো প্রসেসিং এর জন্য। 1 এর দূরত্ব হচ্ছে 1।
1 থেকে যদি আমি 0 এ যাই, তাহলে 0 এর নতুন দূরত্ব হবে 1+1 = 2। কোন দরকার নাই আপডেটের, 0 এর দূরত্ব 0।
1 থেকে যদি আমি 2 এ যাই, তাহলে 2 এর নতুন দূরত্ব হবে 1+1 = 2। 2 কে প্রসেসিং এর জন্য আবার কিউতে ঢুকাই।
1 থেকে যদি আমি 4 এ যাই, তাহলে 4 এর নতুন দূরত্ব হবে 1+5 = 6। 4 কে প্রসেসিং এর জন্য আবার কিউতে ঢুকাই।
এখন আমাদের কিউ এর অবস্থা এই রকম 2,3,2,4
| শহর | দূরত্ব |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 6 |
| 4 | 6 |
আমরা কিউ এর ডগা থেকে 2 কে বের করে আনবো প্রসেসিং এর জন্য। 2 এর দূরত্ব হচ্ছে 2।
2 থেকে যদি আমি 0 এ যাই, তাহলে 0 এর নতুন দূরত্ব হবে 2+3= 5 । কোন দরকার নাই আপডেটের, 0 এর দূরত্ব 0।
2 থেকে যদি আমি 1 এ যাই, তাহলে 1 এর নতুন দূরত্ব হবে 2+1= 3 । কোন দরকার নাই আপডেটের, 1 এর দূরত্ব 1।
2 থেকে যদি আমি 3 এ যাই, তাহলে 3 এর নতুন দূরত্ব হবে 2+2= 4 । 3 কে প্রসেসিং এর জন্য আবার কিউতে ঢুকাই।
2 থেকে যদি আমি 4 এ যাই, তাহলে 4 এর নতুন দূরত্ব হবে 2+2 = 4। 4 কে প্রসেসিং এর জন্য আবার কিউতে ঢুকাই।
এখন আমাদের কিউ এর অবস্থা এই রকম 3,2,4,3,4
| শহর | দূরত্ব |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 4 |
| 4 | 4 |
আমরা কিউ এর ডগা থেকে 3 কে বের করে আনবো প্রসেসিং এর জন্য। 3 এর দূরত্ব হচ্ছে 4।
3 থেকে যদি আমি 3 এ যাই, তাহলে 0 এর নতুন দূরত্ব হবে 4+6= 10 । কোন দরকার নাই আপডেটের, 0 এর দূরত্ব 0।
3 থেকে যদি আমি 2 এ যাই, তাহলে 2 এর নতুন দূরত্ব হবে 4+2= 6। কোন দরকার নাই আপডেটের, 2 এর দূরত্ব 2।
3 থেকে যদি আমি 4 এ যাই, তাহলে 4 এর নতুন দূরত্ব হবে 4+1= 5। কোন দরকার নাই আপডেটের, 4 এর দূরত্ব 4।
এখন আমাদের কিউ এর অবস্থা এই রকম 2,4,3,4
আর দূরত্বগুলো হচ্ছে
| শহর | দূরত্ব |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 4 |
| 4 | 4 |
এরপর কিউ খালি না হওয়া পর্যন্ত লুপ চলতে থাকবে। কিন্তু এরপর আর কোন আপডেট হবে না। কারণ এটাই আসলে 0 থেকে বাকি সব শহরগুলোতে যাবার সবচে’ জন্য কম দূরত্ব।
সিপিপিতে এই অ্যালগরিদমটার ইম্প্লিমেন্টেশন হবে এরকম
vector<int> edge[100], cost[100];
const int infinity = 1000000000;
// edge[i][j] = jth node connected with i
// cost[i][j] = cost of that edge
int bfs(int source, int destination) {
int d[100]; // for storing distance
for (int i = 0; i < 100; i++) d[i] = infinity;
queue<int> q;
q.push(source);
d[source] = 0;
while(!q.empty()) {
int u = q.front(); q.pop();
for (int i = 0; i < edge[u].size(); i++) {
int v = edge[u][i];
// updating (also known as relaxing)
if (d[v] > d[u] + cost[u][i]) {
d[v] = d[u] + cost[u][i];
q.push(v);
}
}
}
return d[destination];
}৪ ডায়াক্সট্রার শর্টেস্ট পাথ অ্যালগরিদম
BFS খুবই ভালো জিনিস। সত্যি কথা আমার ভয়াবহ পছন্দের একটা জিনিস BFS কারণ ধাই ধাই করে BFS কোড লিখে ফেলা যায়, যদি তুমি প্রবলেমটাকে গ্রাফের প্রবলেমে পাল্টাই ফেলতে পারো। অল্প কিছু চালাকি দিয়ে BFS কে ফাস্ট করে ফেলা যায়। একটা হয়তো তুমি এখনই দেখতে পাচ্ছো, একটা শহরকে যদি এরিমধ্যে কিউতে থাকে, ওটাকে আবার কিউতে ঢোকানোর কোন মানে নেই। এ ধরণের চালাকিকে আমরা প্রোগ্রামাররা বলি “প্রুনিঙ” ( pruning )। প্রুনিং এর খাস বাংলা হচ্ছে ছাটাই করা - মানে ধরে ছাটাই করে ছোট করে দেয়া।
BFS এর একটা সমস্যা আছে। সেটা হচ্ছে, যদি এমন হয়, যে আমি শহর 5 কে যখন প্রসেস করলাম তার দূরত্ব পেলাম 100। তো আমি ওর আশে পাশের সব শহরকে আপডেট করলাম। তারপর আরেকটু পর আবার 5 কে পেলাম কিউতে তখন তার দূরত্ব হচ্ছে 50। আমি আবার আশেপাশের সবাইকে আপডেট করলাম। তারপর আবার কিউতে 5 কে পেলাম 40 দূরত্ব নিয়ে।
তো তুমি দেখতে পাচ্ছো, আমাদের আপডেটে একটা সমস্যা আছে - আমরা কিউতে যাকে আগে পাচ্ছি তাকে প্রসেস করছি। তো এভাবে প্রসেস করলে এরকম একটা পরিস্থিতি সম্ভব যেখানে আমরা একই শহরকে বহুবার ভুল দূরত্ব পেয়েও আপডেট করতে থাকবো। ওই শহরের উপর যেসব শহর নির্ভরশীল তারাও বহুবার আপডেট হবে। তাদের উপর যারা নির্ভরশীল তারাও বহুবার আপডেট হবে।
Edsger W. Dijkstra ১৯৫৯ সালে এই ঝামেলা বন্ধ করার একটা পথ খুঁজে পেলো। সে বলল কি, আমরা আরেকটা চালাকি করে দেখতে পারি, কিউ থেকে যখন শহর বের করে আনবো প্রসেস করার জন্য, আমরা সবচে’ কাছের শহরটাকে বের করে আনতে পারি। তাহলে সেই শহরটাকে আর কখনো আরেকবার প্রসেস করা লাগবে না।
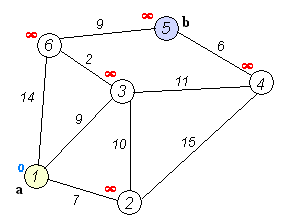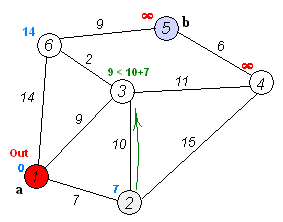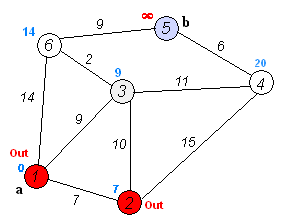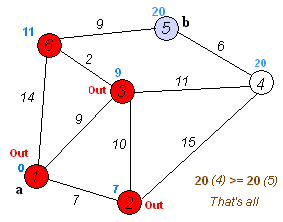
তো আমাদের কাজ হচ্ছে শুধু কিউটা তুলে দিয়ে সেখানে একটা প্রায়োরিটি কিউ বসানোর, সে নোডটা সবচে’ কম দূরত্বে আছে তাকে আমরা সবার আগে প্রসেস করবো - এটা হচ্ছে আমাদের প্রায়েরিটি।
সিপিপি তে একটা সহজ ইম্প্লিমেন্টেশন হবে এরকম -
vector<int> edge[100], cost[100];
const int infinity = 1000000000;
edge[i][j] = jth node connected with i
cost[i][j] = cost of that edge
struct data {
int city, dist;
bool operator < (const data& p) const {
return dist > p.dist;
}
};
int dijkstra(int source, int destination) {
int d[100]; // for storing distance
data u, v;
priority_queue<data> q;
for (int i = 0; i < 100; i++) d[i] = infinity;
u.city = source, u.dist = 0;
q.push(u);
d[source] = 0;
while(!q.empty()) {
u = q.top(); q.pop();
for (int i = 0; i < edge[u.city].size(); i++) {
v.city = edge[u.city][i];
v.dist = cost[u.city][i] + d[u.city];
// relaxing
if(d[v.city] > v.dist) {
d[v.city] = v.dist;
q.push(v);
}
}
}
return d[destination];
}৫ বেলম্যান ফোর্ডের অ্যালগরিদম
গ্রাফটা যদি এরকম হয় তাহলে কি হবে?
আমরা যতবার ইচ্ছা 2-3-4-1 এ পাক খেতে পারি। যতবার পাক খাবো তত আমাদের 0 থেকে 5 এর দূরত্ব কমবে, তাই না? তো এই লুপ অনন্তবার চলতে থাকবে তো চলতে থাকবে। আমাদের BFS তো ফেইল খাবেই খাবে, ডায়াক্সট্রাও ফেইল খাবে।
গ্রাফে যদি নেগেটিভ সাইকেল থাকে - শুধু সেক্ষেত্রেই এই ঝামেলা লাগতেসে। তো এই ক্ষেত্রে আমরা বেলম্যান ফোর্ড ব্যবহার করি। খেয়াল করো, যে একটা কানেক্টেড গ্রাফে যদি একটা নেগেটিভ সাইকেল আমরা পাই, তাহলে গ্রাফটাতে শর্টেস্ট পাথ খোঁজার আর কোন মানে হয় না। বেলম্যান ফোর্ড করে কি যতক্ষণ রিল্যাক্স করা যায়, ততক্ষণ রিল্যাক্স করে। (রিলাক্স মানে আপডেট করা) তারপর রিলাক্স করা শেষে সে দেখে এখনো কোন রিলাক্স করার মতো edge আছে কিনা। n-1 বার প্রতিটা নোড নিয়ে আপডেট করলে, ততক্ষণে সবগুলো আপডেট করার মতো নোড আপডেট হয়ে যাবার কথা। যদি তা না হয়, তার মানে অবশ্যই নেগেটিভ একটা সাইকেল আছে কোথাও।
এখানে রিল্যাক্স করার মানে হচ্ছে যদি এজটা হয় u থেকে v তে আর দৈর্ঘ্য হয় cost[u][v]
if (d[v] > d[u] + cost[u][v]) {
d[v] = d[u] + cost[u][v];
}আমার বেলম্যান ফোর্ড ইম্প্লিমেন্টেশনটা দেখতে এরকম -
#define M 305
#define cycle -33
vector<int> e[M], c[M];
int n, d[M], p[M]; // d is for distance, p for predecessor
int inf = 1<<29; // 2^29, infinity
int bellmanFord(int s, int f) {
for (int i = 0; i < n; i++) {
d[i] = (i == s) ? 0 : inf;
p[i] = -1;
}
// updating the shortest paths
for (int k = 0; i < n; i++) {
bool done = 1;
// the following two loops iterates
// on the whole set of edges
for (int i = 0; i < n; i++) { // for each node i
for (int j = 0; j < e[i].size(); j++) { // each edge of i
int u = i, v = e[i][j], uv = c[i][j]; // simplicity
if (d[u] + uv < d[v]) {
d[v] = d[u] + uv;
p[v] = u; // the best way to come to v is through u
done = false; // found something to update
}
}
}
if (done) break; // there was nothing to update
}
// looking for cycle
for (int i = 0; i < n; i++) { // for each node i
for (int j = 0; j < e[i].size(); j++) { // for each edge of node i
int u = i, v = e[i][j], uv = c[i][j]; // simplicity!
if (d[u] + uv < d[v]) return cycle; // we found cycle
}
}
return d[f];
}৬ ফ্লয়েড ওয়ার্শাল
ফ্লয়েড ওয়ার্শাল এর মূল কন্সেপ্টটা খুব সহজ। তুমি যদি কন্সেপ্টটা বোঝো, তুমি যেকোন ফ্লয়েড ওয়ার্শাল প্রবলেম সলভ করতে পারবে। কিন্তু অ্যালগরিদমটা কেন কাজ করে সেটা বোঝার জন্য তুমি এখানে একটা ঢু মারতে পারো। আমার এই সাধাসিধা টিউটোরিয়ালটা দিয়ে আমি আপাতত কাওকে ভয় পাওয়াতে চাই না কঠিন কিছু লিখে।
আমি যদি i থেকে j তে যেতে চাই তাহলে , হয় আমি সোজা i থেকে j তে যাবো, অথবা কোন একটা k হয়ে j তে যাবো। যখন আমি k হয়ে যাবো তখন আমার i থেকে j এর সবচে’ ছোট দূরত্ব dist[i][j] হবে dist[i][k] + dist[k][j] । এখানে dist[a][b] মানে a থেকে b যাওয়ার সবচে’ ছোট পথটার দূরত্ব। আমি যদি সবগুলো k এর জন্য ট্রাই করি একবার করে, তাহলে আপডেট করতে থাকলে আপডেট করার শেষে অবশ্যই dist[a][b] হবে a থেকে b তে যাওয়ার সবচে’ ছোট পথ।
তাহলে অ্যালগরিদমটা দাড়াচ্ছে এরকম
int d[100][100]; // d[i][j] = distance from i to j
for (int k = 0; k < n; k++)
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++) {
if (d[i][j] > d[i][k] + d[k][j])
d[i][j] = d[i][k] + d[k][j];
}ফ্লয়েড ওয়ার্শালের মজা হচ্ছে এটা লেখা খুব সহজ। সত্যি কথা আমি যখন লিখি কন্টেস্টের সময় ম্যাকরো লাগিয়ে তখন সেটা দেখতে এরকম হয়
REP(k,n) REP(i,n) REP(j,n) d[i][j] = min(d[i][j], d[i][k] + d[k][j]);আর আরেকটা সুবিধা হচ্ছে, বাকি সব অ্যালগরিদম একটা শহরকে ধরে নেয় শুরুর শহর (source), তারপর বাকি সবগুলো শহরের দূরত্ব বের করে ওই শহরটা থেকে। এটাকে আমরা বলি Single Source Shortest Path (SSSP)। ফ্লয়েড ওয়ার্শাল করে কি সবগুলো শহর থেকে সবগুলো শহরের শর্টেস্ট পাথ বের করে ফেলে। তোমার অ্যলগরিদম শেষে তুমি যদি জানতে চাও a থেকে b এর দূরত্ব কত সেটা তুমি dist[a][b] থেকেই পেয়ে যাবে।
৭ টাইম কম্প্লেক্সিটি
খুব রাফলি,
- BFS এর কম্প্লেক্সিটি হচ্ছে $\mathcal{O}(n^{2})$
- ডায়াক্সট্রার কম্প্লেক্সিটি হচ্ছে $\mathcal{O}(nlogn)$
- বেলম্যান ফোর্ড $\mathcal{O}(n^{3})$
- ফ্লয়েড ওয়ার্শাল $\mathcal{O}(n^{3})$
যখন ইনপুটের সাইজ দেখবা, যেটা লিখতে সবচে’ সোজা আর যেই অ্যালগরিদমটা কাজ করবে, সেটা লিখবা। যেমন ধরো n যদি 100 এর ছোট হয়, কোন দরকার নাই BFS লিখে মারা যাবার। একটা ছোট্ট ফ্লয়েড লিখে ফেলো। আবার হিসেব করে যদি দেখো যে BFS এ পোষাচ্ছে ভুলেও ডায়াক্সট্রা লিখতে যেও না। আর খেয়াল রেখো গ্রাফটাতে নেগেটিভ সাইকেল আছে কিনা। যদি থাকে সাবধানে বেলম্যান ফোর্ড লিখে ফেইলো।
৮ উপসংহার
শর্টেস্ট পাথ প্রবলেমগুলোর আসল ব্যাপার হচ্ছে প্রবলেমটাকে গ্রাফে মডেল করা। তারপরে অ্যালগরিদমগুলো ব্যবহার করে শর্টেস্ট পাথ বের করে ফেলা যায়।

